Bode çizimi ve Nyquist çizimleri, özellikle elektrokimyacılar arasında Elektrokimyasal Empedans Spektroskopisi veya EIS verileri için çok popüler çizimlerdir. Bu nedenle, Nyquist Plot, adını İsveçli bir Amerikalı olan “Harry Nyquist” ten almıştır. Kendisi bir elektrik mühendisidir ve bu arsayı 1932 yılında elektronik amaçlar için geliştirmiştir. ÇBS sırasında pek çok bilgi toplanır ve bu toplanan bilgilerin sunulması gerekir. Yani bir resim yüz kelimeden daha fazla bilgi verir. Bu nedenle, bir Elektrokimyasal Empedans Spektroskopisini göstermek için Nyquist grafiği gibi bir grafik gösterim kullanılır. Bu makale hakkında bilgi sağlar Nyquist arsa – çalışma, avantajları ve dezavantajları.
Nyquist Grafik Tanımı
Transfer fonksiyonları için yaygın olarak kullanılan grafik gösterim, Nyquist grafiği olarak bilinir. Bu, kontrol sistemini geri besleme kararlılığı ile değerlendirmek için kullanılan bir frekans yanıtı grafiğidir. Frekans parametresi belirli bir aralık boyunca taradığından, karmaşık düzlem içindeki bir transfer fonksiyonunun gerçek ve hayali kısmı için parametrik bir çizimdir. Kartezyen koordinatlarda, nyquist grafiği transfer fonksiyonunun gerçek kısmı X ekseninde, transfer fonksiyonunun hayali kısmı ise Y ekseninde çizilir.
Nyquist Grafiği, otomatik kontrolde ve kararlılık analizi için sinyal işlemede kullanılır çünkü herkes, negatif geri beslemeli bir döngünün Nyquist'in kararlılık ilkesini karşılayıp karşılamadığını anında doğrulayabilir. Nyquist grafiği ise açık döngü kontrol sistemi eşdeğer kapalı döngü sistemi kararsız hale geldikten sonra yaklaşık olarak gerçek eksen üzerindeki noktayı kapsar.
Nyquist Çizim Grafiği
Nyquist çizim grafikleri, esas olarak noktayı bulmak için kullanılan kutupsal çizimlerin uzantısıdır. kapalı döngü kontrol sistemleri basitçe 'ω'yi −∞'dan ∞'ye değiştirerek kararlılık. Bu, bu grafiklerin çoğunlukla açık çevrim transfer fonksiyonunun toplam frekans yanıtını çizmek için kullanıldığı anlamına gelir. Nyquist grafiği, kontrol sisteminin kararlılığını geri bildirimle basitçe değerlendirir. Dolayısıyla, bir Kartezyen koordinat sisteminde, transfer fonksiyonunun gerçek par değeri basitçe X ekseni üzerine çizilirken sanal kısım basitçe Y ekseni üzerine çizilir.
Benzer Nyquist grafiği, transfer fonksiyonunun kazancının radyal koordinat olduğu ve transfer fonksiyonunun fazının eşdeğer açısal koordinat olduğu kutupsal koordinatlarla basitçe açıklanabilir.
Nyquist grafiği, kullanılan bazı terminolojiler bilinerek anlaşılabilir. Nyquist grafiğinde, karmaşık bir düzlem içindeki kapalı bir yol, kontur olarak bilinir.
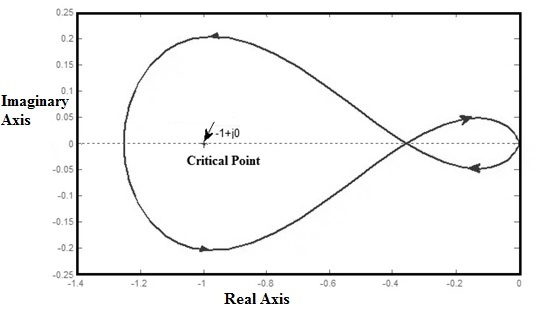
Nyquist Yolu
Nyquist yolu veya Nyquist Çevresi, s düzleminin sağ tarafını tamamen çevreleyen s düzlemi içinde kapalı bir konturdur. Uçağın toplam RHS'sini çevrelemek için, kaynaktaki 'jω' ekseni ve merkezi boyunca bir çapla büyük bir yarım daire şeridi çizilir. Yarım daire yarıçapı basitçe Nyquist Çevreleme olarak ele alınır.

Nyquist Kuşatması
Eğride bulunan bir noktanın bir çizgi ile çevrelendiği bilinmektedir.
Nyquist Haritalama
s-düzlemi içindeki bir noktanın F(s) düzlemi içindeki bir noktaya dönüştürüldüğü prosedür eşleme olarak bilinir ve F(s) eşleme işlevi olarak bilinir.
Geri beslemeli kontrol sisteminin kararlılık analizi, temel olarak s-düzleminin üzerindeki karakteristik denklem için konum köklerinin tanınmasına bağlıdır.
Böylece, s düzlemindeki kök sol yüzde bulunuyorsa, kontrol sistemi kararlıdır. Böylece, sistemin bağıl kararlılığı, Nyquist grafiği, Bode grafiği ve Nichols grafiği gibi farklı frekans yanıtı teknikleri ile belirlenebilir.
Nyquist Stabilite Kriteri
Nyquist kararlılık kriteri, temel olarak, S-düzleminin belirli bölgesindeki karakteristik bir denklem için köklerin varlığını tanımak için kullanılır. N = Z – P gibi Nyquist kararlılık kriteri basitçe bunu söylüyor. 'N', orijine ilişkin toplam çevre sayısıdır, 'P' kutup sayısıdır ve 'Z' toplam sıfır sayısıdır.
Durum 1'de: N = 0 (kuşatma yok) olduğunda, böylece Z = P = 0 & Z = P.
N = 0 ise, sistemin kararlı olması için P '0' olmalıdır.
Durum 2'de: N, 0'dan büyük olduğunda (saat yönünde çevreleme), dolayısıyla P = 0, Z ≠0 & Z > P
Bu iki durumda sistem kararsızdır.
Durum 3'te: N, 0'dan küçük olduğunda (saat yönünün tersine çevreleme), dolayısıyla Z = 0, P ≠0 & P > Z
Böylece sistem kararlıdır.
Nyquist Grafiği Nasıl Çizilir?
Aşağıda tartışılan nyquist grafiğinin çizilmesiyle ilgili birçok adım vardır.
- 1. adımda: 's' düzleminde G(s)H(s) gibi bir açık döngü transfer fonksiyonu için kutupları kontrol etmeniz gerekir.
- Adım 2'de: R'nin sonsuza gitme eğiliminde olduğu 'R' yarıçaplı bir yarım daire çizerek s düzleminin tüm sağ tarafını dahil ederek doğru Nyquist konturunu seçin.
- 3. adımda: Nyquist yolunun konumu ile anahat üzerindeki farklı segmentleri tanıyın.
- Adım 4'te: Haritalama segmentinin, haritalama fonksiyonunda ilgili segment denklemini basitçe değiştirerek segment boyunca çalışması gerekir. Genel olarak, belirli bir segment için kutup grafiklerini çizmemiz gerekir.
- 5. adımda: Genel olarak, segment eşleme, pozitif hayali eksenin belirli yolu için eşlemenin yansıma görüntülerini oluşturur.
- 6. adımda: Düzlemin sağ yarısını kaplayan yarım daire biçimli şerit, normalde G(s) H(s) düzlemi içindeki bir noktaya eşlenir.
- 7. adımda: Gerekli Nyquist diyagramını elde etmek için tüm çeşitli haritalama segmentlerini birbirine bağlayın.
- 8. adımda: Hayır'a dikkat edin. (-1, 0) civarında saat yönünde çevrelemeler ve N = Z – P aracılığıyla kararlılığa karar verin.
Nyquist grafiği çizildiğinde, kapalı döngü kontrol sisteminin kararlılığını Nyquist kararlılık kriteri ile keşfedebiliriz. Dolayısıyla, kritik nokta (-1+j0) kuşatmanın dışında yer alıyorsa, kapalı çevrim kontrol sistemi tamamen kararlıdır.
Açık döngü transfer fonksiyonu G(S)H(S) = N(S)/D(S) şeklindedir.
Kapalı çevrim transfer fonksiyonu G(S)/1+ G(S)H(S)'dir.
N(s) = sıfır, açık döngü sıfırdır ve D(s) açık döngü kutbudur.
Stabilite açısından, s-düzleminin sağ yüzünde hiçbir kapalı döngü kutbu bulunmamalıdır. 1 + G(s) H(s) sıfıra eşit gibi özellik denklemi, kapalı çevrim kutuplarını ifade eder.
1 + G(s) H(s) sıfıra eşit olduğunda q(s) sıfır olmalıdır.
Dolayısıyla, kararlılık bakış açısından, q(s)'nin sıfırları s-düzleminin Sağ El Düzleminde yer almamalıdır.
Gücü tanımlamak için, tüm RHP'nin dikkate alınması gerekir. Bu nedenle, sonsuza gitme eğiliminde olan 'R' yarım daire yarıçapını göz önünde bulundurarak, RHP içindeki tüm noktaları içeren bir yarım daire hayal ediyoruz.
Nyquist Plot ile Stabilite Analizi
Nyquist grafiğinden, parametre değerlerine bağlı olarak kontrol sisteminin kararlı mı, kararsız mı yoksa marjinal olarak kararlı mı olduğunu anlayabiliriz.
- Geçiş frekansı ve faz geçiş frekansı kazanın.
- Marj ve faz marjı kazanın.
Faz Geçiş Frekansı.
Nyquist grafiğinin negatif gerçek eksenle buluştuğu noktadaki frekansa faz geçiş frekansı denir ve ωpc ile gösterilir.
Geçiş Frekansı Kazanın
Nyquist grafiğinin bir büyüklüğe sahip olduğu noktada frekans, kazanç geçiş frekansı olarak adlandırılır ve ωgc ile gösterilir.
Faz geçişi ve kazanç geçişi gibi iki frekans arasındaki ana ilişkiye dayanan kontrol sistemi kararlılığı aşağıda tartışılmaktadır.
- ωpc, ωgc'ye kıyasla daha yüksekse, kontrol sistemi kararlıdır.
- ωpc, ωgc'ye eşitse, kontrol sistemi biraz kararlıdır.
- ωpc, ωgc'ye kıyasla daha küçükse, kontrol sistemi kararlı değildir.
Kazanç Marjı
Kazanç marjı, faz geçiş frekansındaki Nyquist grafiğinin büyüklüğünün tersine eşdeğerdir.
Kazanç marjı (GM) =1/Mpc
Burada 'Mpc', ωpc veya faz geçiş frekansında normal ölçekteki büyüklüktür.
Faz Marjı
Faz marjı, 180 derecenin toplamına ve ωgc veya kazanç geçiş frekansındaki faz açısına eşdeğerdir.
PM = 1800 + ϕgc
Burada ϕgc, kazanç geçiş frekansındaki (ωgc) faz açısıdır.
Kontrol sisteminin kararlılığı, aşağıda verilen kazanç marjı ve faz marjı gibi iki marj arasındaki ana ilişkiye bağlıdır.
Kazanç marjı birden yüksekse ve faz marjı pozitifse, kontrol sistemi kararlıdır.
Kazanç marjı bire eşitse ve faz marjı '0' derece ise, kontrol sistemi biraz kararlıdır.
Kazanç marjı birden düşükse ve faz marjı negatifse, kontrol sistemi kararlı değildir.
Nyquist Plot Örnek Problemleri
Ör1: Nyquist grafiği negatif gerçek ekseni 0,6 mesafede keserse, sistemin kazanç marjı nedir?
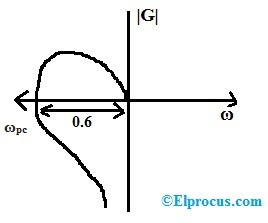
Sistemin kazanç marjının, kapalı döngü sistemini kararsız hale getirmek için açık döngü kazancında gerekli olan değişiklik miktarı olarak tanımlanabileceğini biliyoruz.
Kazanç marjı veya GM = 1/|G| wpc
Burada sistemin kazancı |G| ve wpc, faz geçiş frekansıdır.
Faz geçiş frekansı şu şekilde tanımlanabilir; sistem kazancının '0' olduğu noktadaki frekans.
Gm = 1/0,6 = 1,66
Ör2: Birlik kazanç negatif geribesleme sisteminin açık çevrim sistem transfer fonksiyonu G(s) = 1/S(S+1) olarak verilebilir. S-düzlemindeki Nyquist eğrisi, sağ taraftaki düzlemin tamamını ve aşağıdaki grafikte gösterilen sol taraftaki orijinin etrafındaki küçük alanı içerir. Hayır. (-1+ j0) noktasının G(S) Nyquist grafiği boyunca çevrelenmesinin, 'N' ve ardından 'N' olarak gösterilen Nyquist konturuna eşdeğer?
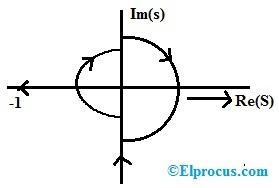
Hayır. (-1+ j0) önemli noktası için çevrelerin sayısı N = P-Z ile verilir.
Burada 'N', bu kritik noktanın saat yönünün tersine çevrilme sayısıdır.
'P', S düzleminin sağ tarafındaki açık döngü kutuplarının sayısıdır.
'Z', S düzleminin sağ tarafındaki kapalı döngü kutuplarının sayısıdır.
Z = 0 kararlılığı için N = P.
Yukarıda verilen formül, yalnızca S düzleminin sağ tarafı için Nyquist eğrisi tanımlandığında ve kutuplar kaynakta hariç tutulduğunda geçerlidir. Eğri dönüşü saat yönünde olmalıdır ve kritik noktanın çevresi saat yönünün tersine olmalıdır.
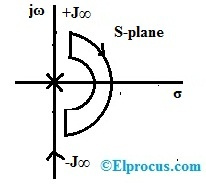
G(s) = 1/S(S+1).
Açık döngü kutupları S = 0,-1'de mevcuttur
Kapalı çevrimin transfer fonksiyonu = 1/S^2+S+1
Sağ taraftaki kapalı direğin sayısı sıfırdır.
Ancak Nyquist konturu, S düzleminin toplam yarım kenarı için tanımlanır ve orijindeki kutbu da içerir.
Böylece, S=0'da açık döngü kutbu, S düzleminin sağ tarafı içindeki kutup olarak kabul edilir.
N = P-Z =>1-0 =>1
Avantajlar ve dezavantajlar
bu Nyquist grafiğinin avantajları aşağıdakileri dahil edin.
- Nyquist grafiği, sistem kararlılığının belirlenmesinde son derece yararlı bir araçtır.
- Sadece zaman gecikmelerini yönetebildiği için Routh-Horwitz ve kök yerine göre birçok avantajı vardır.
- Ancak, stabiliteye karar vermek için Bode çizimini kullanmamız için bize bir yöntem sağladığı için çok faydalıdır.
- Bunu kullanarak, kontrol sistemi kararlılığına karar verilebilir.
- Bir açık döngü transfer fonksiyonu, sadece frekans yanıtı ölçülerek bulunur.
- Zaman gecikmesi açısından kök yerine kıyasla daha iyidir, bu da Nyquist grafiğinin sistem içindeki zaman gecikmesini kolayca yönetebileceği anlamına gelir.
- Açık çevrim transfer fonksiyonunun frekans cevabını bulabilir.
- Hayır'ı bulur. s-düzleminin sağ yüzünde bulunan kutupların sayısı.
- Sistemin bağıl kararlılığını/
bu Nyquist grafiğinin dezavantajları aşağıdakileri dahil edin.
- Nyquist çizimi bazı zor matematiksel yöntemler kullanır.
- Sistemin tüm gücünü çözemez.
- s düzleminin sağ yüzündeki mevcut kutuplar hakkında kesin bilgi vermez.
Nyquist Grafik Uygulamaları
Nyquist grafiğinin uygulamaları aşağıdakileri içerir.
- Nyquist grafiği, frekans alanı içindeki grafiksel bir süreç aracılığıyla sistem kararlılığını oluşturmak için kullanılır.
- Bir Nyquist grafiği veya bir frekans yanıt grafiği, esas olarak kontrol mühendisliği ve sinyal işlemede kullanılır.
- Bunlar, kapalı döngü kontrol sistemi kararlılığını bulmak için kullanılan kutup grafiklerinin uzantısıdır.
- Sistem kararlılığının belirlenmesinde son derece yararlı bir araçtır.
- Bir Nyquist grafiği kullanarak, iki nokta (–1, 0) arasındaki mesafeyi ve eğrinin negatif gerçek ekseni kestiği noktayı izleyebiliriz.
Kararlılığı Belirlemek için Nyquist Grafiği nasıl kullanılır?
Kararlılık, Nyquist Grafiği kullanılarak basitçe no'ya bakılarak belirlenebilir. noktasının çevrelenmesi (−1, 0). Gerçek eksen geçişlerine bakılarak sistemin kararlı olacağı kazançların çeşitliliği belirlenebilir. Bu çizim, transfer fonksiyonunun şekli ile ilgili bazı veriler sağlar.
Örnekleme için Nyquist Kriterleri nelerdir?
Nyquist kriterleri, örnekleme frekansının, sinyalde bulunan maksimum frekansın minimum iki katı olmasını gerektirir. Örnekleme frekansı, en yüksek analog sinyal frekansının iki katından düşükse, örtüşme adı verilen bir olay meydana gelir.
Nyquist Grafiği için ne kullanılır?
Nyquist Plot için bir açık döngü transfer fonksiyonu kullanılır.
Nyquist Kuralı nedir?
Nyquist kuralı basitçe, periyodik bir sinyalin, sinyalin maksimum frekans bileşeninin iki katının üzerinde örneklenmesi gerektiğini belirtir. Aslında, mevcut zaman sınırlı olduğundan, örnekleme oranı gerekenden biraz daha yüksektir.
Gürültüsüz için Nyquist Bit Hızı Formülü nedir?
Nyquist basitçe, bir 'B' bant genişliği kanalında, her saniye için 2B'ye kadar ortogonal sinyal iletebileceğinizi, yani 'Rp'nin nabız hızı olduğu her yerde Rp ≤ 2B olduğunu belirtir.
Nyquist'in Planı Neyi Temsil Eder?
Nyquist grafiği, transfer fonksiyonunun formuyla ilgili bazı bilgileri temsil eder. Yani mesela; bu arsa no arasındaki varyasyon hakkında bilgi verir. eğrinin orijine ulaştığı açı boyunca transfer fonksiyonunun kutupları ve sıfırları.
Böylece, bu Nyquist planına genel bakış – avantajları, dezavantajları ve uygulamaları. Nyquist grafikleri, kontrol sisteminin kararlılık, faz marjı ve kazanç marjı gibi özelliklerini analiz etmek için kullanılır. Matlab kullanarak Nyquist Grafiği adinamik model aracılığıyla üretilen frekans yanıtıyla ilgili bir Nyquist çizim grafiği oluşturmamıza yardımcı olur. İşte size bir soru, bode arsa nedir?